
Daftar Isi:
- Pengarang John Day [email protected].
- Public 2024-01-30 09:59.
- Terakhir diubah 2025-01-23 14:49.
pengantar
Panduan ini ditujukan untuk semua orang yang tertarik menggunakan Akselerometer dan Giroskop serta perangkat kombinasi IMU (Unit Pengukuran Inersia) dalam proyek elektronik mereka
Kami akan membahas:
- Apa yang diukur akselerometer?
- Apa yang diukur dengan giroskop (alias gyro)?
- Bagaimana mengkonversi pembacaan analog-ke-digital (ADC) yang Anda dapatkan dari sensor ini ke unit fisik (itu akan menjadi g untuk akselerometer, deg/s untuk giroskop)
- Cara menggabungkan pembacaan akselerometer dan giroskop untuk mendapatkan informasi akurat tentang kemiringan perangkat Anda relatif terhadap bidang tanah
Sepanjang artikel saya akan mencoba untuk menjaga matematika untuk minimum. Jika Anda tahu apa itu Sinus/Cosinus/Singgung maka Anda harus dapat memahami dan menggunakan ide-ide ini dalam proyek Anda, apa pun platform yang Anda gunakan: Arduino, Propeller, Basic Stamp, Atmel chips, Microchip PIC, dll.
Ada orang di luar sana yang percaya bahwa Anda memerlukan matematika kompleks untuk menggunakan unit IMU (filter FIR atau IIR kompleks seperti filter Kalman, filter Parks-McClellan, dll). Anda dapat meneliti semua itu dan mencapai hasil yang luar biasa namun kompleks. Cara saya menjelaskan sesuatu hanya membutuhkan matematika dasar. Saya sangat percaya pada kesederhanaan. Saya pikir sistem yang sederhana lebih mudah untuk dikontrol dan dipantau, selain itu banyak perangkat tertanam tidak memiliki kekuatan dan sumber daya untuk mengimplementasikan algoritma kompleks yang membutuhkan perhitungan matriks.
Saya akan menggunakan sebagai contoh unit IMU baru, Accelerometer Acc_Gyro + IMU Gyro. Kami akan menggunakan parameter perangkat ini dalam contoh kami di bawah ini. Unit ini adalah perangkat yang baik untuk memulai karena terdiri dari 2 perangkat:
- LIS331AL (lembar data) - akselerometer 2G triaksial - LPR550AL (lembar data) - pitch and roll sumbu ganda, giroskop 500 deg/dtk
Bersama-sama mereka mewakili Unit Pengukuran Inersia 5 Derajat Kebebasan. Sekarang itu nama yang mewah! Namun demikian, di balik nama mewah tersebut terdapat perangkat kombinasi yang sangat berguna yang akan kami bahas dan jelaskan secara rinci dalam panduan ini.
Langkah 1: Akselerometer
Untuk memahami unit ini kita akan mulai dengan akselerometer. Saat memikirkan akselerometer, seringkali berguna untuk membayangkan sebuah kotak berbentuk kubus dengan bola di dalamnya. Anda mungkin membayangkan sesuatu yang lain seperti kue atau donat, tetapi saya akan membayangkan sebuah bola:
Jika kita mengambil kotak ini di tempat tanpa medan gravitasi atau dalam hal ini tanpa medan lain yang dapat mempengaruhi posisi bola - bola hanya akan mengapung di tengah kotak. Anda dapat membayangkan kotak itu berada di luar angkasa jauh-jauh dari benda kosmik mana pun, atau jika tempat seperti itu sulit ditemukan, bayangkan setidaknya sebuah pesawat ruang angkasa yang mengorbit di sekitar planet di mana semuanya dalam keadaan tanpa bobot. Dari gambar di atas Anda dapat melihat bahwa kami menetapkan sepasang dinding pada setiap sumbu (kami menghapus dinding Y+ sehingga kami dapat melihat ke dalam kotak). Bayangkan bahwa setiap dinding peka terhadap tekanan. Jika kita memindahkan kotak secara tiba-tiba ke kiri (dipercepat dengan percepatan 1g = 9,8m/s^2), bola akan membentur dinding X-. Kami kemudian mengukur gaya tekanan yang diberikan bola ke dinding dan menghasilkan nilai -1g pada sumbu X.
Harap dicatat bahwa akselerometer sebenarnya akan mendeteksi gaya yang diarahkan ke arah yang berlawanan dari vektor percepatan. Gaya ini sering disebut Gaya Inersia atau Gaya Fiksi. Satu hal yang harus Anda pelajari dari ini adalah bahwa akselerometer mengukur percepatan secara tidak langsung melalui gaya yang diterapkan ke salah satu dindingnya (menurut model kami, mungkin pegas atau sesuatu yang lain dalam akselerometer kehidupan nyata). Gaya ini dapat disebabkan oleh percepatan, tetapi seperti yang akan kita lihat pada contoh berikut ini tidak selalu disebabkan oleh percepatan.
Jika kita mengambil model kita dan meletakkannya di Bumi, bola akan jatuh di dinding Z dan akan menerapkan gaya 1g di dinding bawah, seperti yang ditunjukkan pada gambar di bawah ini:
Dalam hal ini kotak tidak bergerak tetapi kita masih mendapatkan pembacaan -1g pada sumbu Z. Tekanan yang diberikan bola pada dinding disebabkan oleh gaya gravitasi. Secara teori, ini bisa menjadi jenis gaya yang berbeda - misalnya, jika Anda membayangkan bola kita terbuat dari logam, menempatkan magnet di sebelah kotak dapat menggerakkan bola sehingga mengenai dinding lain. Hal ini dikatakan hanya untuk membuktikan bahwa pada dasarnya akselerometer mengukur gaya bukan percepatan. Kebetulan bahwa akselerasi menyebabkan gaya inersia yang ditangkap oleh mekanisme deteksi gaya akselerometer.
Meskipun model ini tidak persis bagaimana sensor MEMS dibangun, seringkali berguna dalam memecahkan masalah terkait akselerometer. Sebenarnya ada sensor serupa yang memiliki bola logam di dalamnya, yang disebut sakelar kemiringan, namun lebih primitif dan biasanya hanya dapat mengetahui apakah perangkat miring dalam rentang tertentu atau tidak, bukan tingkat kemiringan.
Sejauh ini kami telah menganalisis output akselerometer pada satu sumbu dan hanya ini yang akan Anda dapatkan dengan akselerometer sumbu tunggal. Nilai sebenarnya dari akselerometer triaksial berasal dari fakta bahwa mereka dapat mendeteksi gaya inersia pada ketiga sumbu. Mari kembali ke model kotak kita, dan putar kotak 45 derajat ke kanan. Bola akan menyentuh 2 dinding sekarang: Z- dan X- seperti terlihat pada gambar di bawah ini:
Nilai 0,71 tidak sembarang, mereka sebenarnya merupakan perkiraan untuk SQRT(1/2). Ini akan menjadi lebih jelas saat kami memperkenalkan model akselerometer berikutnya.
Pada model sebelumnya kita telah memperbaiki gaya gravitasi dan memutar kotak imajiner kita. Dalam 2 contoh terakhir kami telah menganalisis output dalam 2 posisi kotak yang berbeda, sedangkan vektor gaya tetap konstan. Meskipun ini berguna dalam memahami bagaimana akselerometer berinteraksi dengan gaya luar, akan lebih praktis untuk melakukan perhitungan jika kita menetapkan sistem koordinat ke sumbu akselerometer dan membayangkan bahwa vektor gaya berputar di sekitar kita.
Silakan lihat model di atas, saya mempertahankan warna sumbu sehingga Anda dapat membuat transisi mental dari model sebelumnya ke yang baru. Bayangkan saja bahwa setiap sumbu dalam model baru tegak lurus terhadap masing-masing wajah kotak pada model sebelumnya. Vektor R adalah vektor gaya yang diukur oleh akselerometer (bisa berupa gaya gravitasi atau gaya inersia dari contoh di atas atau kombinasi keduanya). Rx, Ry, Rz adalah proyeksi vektor R pada sumbu X, Y, Z. Harap perhatikan hubungan berikut:
R^2 = Rx^2 + Ry^2 + Rz^2 (Persamaan 1)
yang pada dasarnya setara dengan teorema Pythagoras dalam 3D.
Ingatlah bahwa sedikit sebelumnya saya memberi tahu Anda bahwa nilai SQRT(1/2) ~ 0,71 tidak acak. Jika Anda memasukkannya ke dalam rumus di atas, setelah mengingat bahwa gaya gravitasi kita adalah 1 g, kita dapat memverifikasi bahwa:
1^2 = (-SQRT(1/2))^2 + 0 ^2 + (-SQRT(1/2))^2
cukup dengan mensubstitusi R=1, Rx = -SQRT(1/2), Ry = 0, Rz = -SQRT(1/2) pada Persamaan.1
Setelah pembukaan teori yang panjang, kita semakin dekat dengan akselerometer kehidupan nyata. Nilai Rx, Ry, Rz sebenarnya terkait linier dengan nilai yang akan dihasilkan oleh akselerometer kehidupan nyata Anda dan yang dapat Anda gunakan untuk melakukan berbagai perhitungan.
Sebelum kita sampai di sana, mari kita bicara sedikit tentang cara akselerometer mengirimkan informasi ini kepada kita. Sebagian besar akselerometer terbagi dalam dua kategori: digital dan analog. Akselerometer digital akan memberi Anda informasi menggunakan protokol serial seperti I2C, SPI atau USART, sedangkan akselerometer analog akan mengeluarkan tingkat tegangan dalam rentang yang telah ditentukan yang harus Anda ubah ke nilai digital menggunakan modul ADC (konverter analog ke digital). Saya tidak akan membahas banyak detail tentang cara kerja ADC, sebagian karena topik ini sangat luas dan sebagian karena berbeda dari satu platform ke platform lainnya. Beberapa mikrokontroler akan memiliki modul ADC built-in, beberapa di antaranya akan membutuhkan komponen eksternal untuk melakukan konversi ADC. Apa pun jenis modul ADC yang Anda gunakan, Anda akan mendapatkan nilai dalam rentang tertentu. Misalnya modul ADC 10-bit akan menampilkan nilai dalam kisaran 0..1023, perhatikan bahwa 1023 = 2^10 -1. Modul ADC 12-bit akan menampilkan nilai dalam kisaran 0..4095, perhatikan bahwa 4095 = 2^12-1.
Mari kita lanjutkan dengan mempertimbangkan contoh sederhana, misalkan modul ADC 10bit kami memberi kami nilai berikut untuk tiga saluran akselerometer (sumbu):
AdcRx = 586 AdcRy = 630 AdcRz = 561
Setiap modul ADC akan memiliki tegangan referensi, mari kita asumsikan dalam contoh kita adalah 3.3V. Untuk mengubah nilai adc 10bit menjadi tegangan, kami menggunakan rumus berikut:
VoltsRx = AdcRx * Vref / 1023
Catatan singkat di sini: bahwa untuk ADC 8bit pembagi terakhir adalah 255 = 2 ^ 8 -1, dan untuk ADC 12bit pembagi terakhir adalah 4095 = 2^12 -1.
Menerapkan rumus ini ke semua 3 saluran, kami mendapatkan:
VoltsRx = 586 * 3.3V / 1023 =~ 1.89V (kami membulatkan semua hasil menjadi 2 titik desimal) VoltsRy = 630 * 3.3V / 1023 =~ 2.03V VoltsRz = 561 * 3.3V / 1023 =~ 1.81V
Setiap akselerometer memiliki level tegangan nol-g, Anda dapat menemukannya dalam spesifikasi, ini adalah tegangan yang sesuai dengan 0g. Untuk mendapatkan nilai tegangan yang ditandatangani kita perlu menghitung pergeseran dari level ini. Katakanlah level tegangan 0g kita adalah VzeroG = 1.65V. Kami menghitung pergeseran tegangan dari tegangan nol-g sebagai berikut::
DeltaVoltsRx = 1,89V - 1,65V = 0,24V DeltaVoltsRy = 2,03V - 1,65V = 0,38V DeltaVoltsRz = 1,81V - 1,65V = 0,16V
Kami sekarang memiliki pembacaan accelerometer kami di Volt, itu masih tidak dalam g (9,8 m/s^2), untuk melakukan konversi akhir kami menerapkan sensitivitas accelerometer, biasanya dinyatakan dalam mV/g. Katakanlah Sensitivitas kita = 478.5mV/g = 0.4785V/g. Nilai sensitivitas dapat ditemukan dalam spesifikasi akselerometer. Untuk mendapatkan nilai gaya akhir yang dinyatakan dalam g, kami menggunakan rumus berikut:
Rx = DeltaVoltsRx / Sensitivitas
Rx = 0,24V / 0,4785V/g =~ 0,5g Ry = 0,38V / 0,4785V/g =~ 0,79g Rz = 0,16V / 0,4785V/g =~ 0,33g
Kita tentu saja dapat menggabungkan semua langkah dalam satu rumus, tetapi saya telah melalui semua langkah untuk memperjelas bagaimana Anda beralih dari pembacaan ADC ke komponen vektor gaya yang dinyatakan dalam g.
Rx = (AdcRx * Vref / 1023 - VzeroG) / Sensitivitas (Persamaan 2) Ry = (AdcRy * Vref / 1023 - VzeroG) / Sensitivitas Rz = (AdcRz * Vref / 1023 - VzeroG) / Sensitivitas
Kami sekarang memiliki semua 3 komponen yang menentukan vektor gaya inersia kami, jika perangkat tidak tunduk pada gaya lain selain gravitasi, kami dapat menganggap ini adalah arah vektor gaya gravitasi kami. Jika Anda ingin menghitung kemiringan perangkat relatif terhadap tanah, Anda dapat menghitung sudut antara vektor ini dan sumbu Z. Jika Anda juga tertarik dengan arah kemiringan per sumbu, Anda dapat membagi hasil ini menjadi 2 komponen: kemiringan pada sumbu X dan Y yang dapat dihitung sebagai sudut antara vektor gravitasi dan sumbu X / Y. Menghitung sudut-sudut ini lebih sederhana daripada yang mungkin Anda pikirkan, sekarang kita telah menghitung nilai untuk Rx, Ry, dan Rz. Mari kembali ke model akselerometer terakhir kita dan lakukan beberapa notasi tambahan:
Sudut yang kita minati adalah sudut antara sumbu X, Y, Z dan vektor gaya R. Kita akan mendefinisikan sudut-sudut ini sebagai Axr, Ayr, Azr. Anda dapat melihat dari segitiga siku-siku yang dibentuk oleh R dan Rx bahwa:
cos(Axr) = Rx / R, dan sama: cos(Ayr) = Ry / R cos(Azr) = Rz / R
Kita dapat mengurangi dari Persamaan.1 bahwa R = SQRT(Rx^2 + Ry^2 + Rz^2).
Sekarang kita dapat menemukan sudut kita dengan menggunakan fungsi arccos() (fungsi invers cos()):
Axr = arccos(Rx/R) Ayr = arccos(Ry/R) Azr = arccos(Rz/R)
Kami telah pergi jauh untuk menjelaskan model akselerometer, hanya untuk sampai pada formula ini. Bergantung pada aplikasi Anda, Anda mungkin ingin menggunakan formula perantara apa pun yang telah kami peroleh. Kami juga akan segera memperkenalkan model giroskop, dan kami akan melihat bagaimana data akselerometer dan giroskop dapat digabungkan untuk memberikan estimasi kemiringan yang lebih akurat.
Tapi sebelum kita melakukannya, mari kita lakukan beberapa notasi yang lebih berguna:
cosX = cos(Axr) = Rx / R nyaman = cos(Ayr) = Ry / R cosZ = cos(Azr) = Rz / R
Triplet ini sering disebut Cosinus Arah, dan pada dasarnya mewakili vektor satuan (vektor dengan panjang 1) yang memiliki arah yang sama dengan vektor R kita. Anda dapat dengan mudah memverifikasi bahwa:
SQRT(cosX^2 + cosY^2 + cosZ^2) = 1
Ini adalah properti yang bagus karena membebaskan kita dari pemantauan modulus (panjang) vektor R. Sering kali jika kita hanya tertarik pada arah vektor inersia kita, masuk akal untuk menormalkan modulusnya untuk menyederhanakan perhitungan lainnya.
Langkah 2: Giroskop
Kami tidak akan memperkenalkan model kotak yang setara untuk giroskop seperti yang kami lakukan untuk akselerometer, sebaliknya kami akan langsung beralih ke model akselerometer kedua dan kami akan menunjukkan apa yang diukur giroskop menurut model ini.
Setiap saluran giroskop mengukur rotasi di sekitar salah satu sumbu. Misalnya giroskop 2 sumbu akan mengukur rotasi di sekitar (atau beberapa orang mungkin mengatakan "tentang") sumbu X dan Y. Untuk mengekspresikan rotasi ini dalam angka mari kita lakukan beberapa notasi. Pertama mari kita definisikan:
Rxz - adalah proyeksi vektor gaya inersia R pada bidang XZ Ryz - adalah proyeksi vektor gaya inersia R pada bidang YZ
Dari segitiga siku-siku yang dibentuk oleh Rxz dan Rz, dengan menggunakan teorema Pythagoras diperoleh:
Rxz^2 = Rx^2 + Rz^2, dan juga: Ryz^2 = Ry^2 + Rz^2
juga perhatikan bahwa:
R^2 = Rxz^2 + Ry^2, ini dapat diturunkan dari Persamaan.1 dan persamaan di atas, atau dapat diturunkan dari segitiga siku-siku yang dibentuk oleh R dan Ryz R^2 = Ryz^2 + Rx^2
Kami tidak akan menggunakan rumus ini dalam artikel ini, tetapi berguna untuk mencatat hubungan antara semua nilai dalam model kami.
Sebagai gantinya kita akan mendefinisikan sudut antara sumbu Z dan Rxz, vektor Ryz sebagai berikut:
Axz - adalah sudut antara Rxz (proyeksi R pada bidang XZ) dan sumbu Z Ayz - adalah sudut antara Ryz (proyeksi R pada bidang YZ) dan sumbu Z
Sekarang kita semakin dekat dengan apa yang diukur oleh giroskop. Giroskop mengukur laju perubahan sudut yang ditentukan di atas. Dengan kata lain akan menghasilkan nilai yang berhubungan secara linier dengan laju perubahan sudut-sudut tersebut. Untuk menjelaskan hal ini, mari kita asumsikan bahwa kita telah mengukur sudut rotasi di sekitar sumbu Y (yang akan menjadi sudut Axz) pada waktu t0, dan kita mendefinisikannya sebagai Axz0, selanjutnya kita mengukur sudut ini di lain waktu t1 dan itu adalah Axz1. Tingkat perubahan akan dihitung sebagai berikut:
NilaiAxz = (Axz1 - Axz0) / (t1 - t0).
Jika kita menyatakan Axz dalam derajat, dan waktu dalam detik, maka nilai ini akan dinyatakan dalam derajat/s. Inilah yang diukur oleh giroskop.
Dalam praktiknya, giroskop (kecuali giroskop digital khusus) jarang memberikan nilai yang dinyatakan dalam derajat/s. Sama seperti untuk akselerometer, Anda akan mendapatkan nilai ADC yang harus Anda konversi ke derajat/dtk menggunakan rumus yang mirip dengan Persamaan. 2 yang telah kami definisikan untuk akselerometer. Mari kita perkenalkan rumus konversi ADC ke deg/s untuk giroskop (kita asumsikan kita menggunakan modul ADC 10bit, untuk ADC 8bit ganti 1023 dengan 255, untuk ADC 12bit ganti 1023 dengan 4095).
RateAxz = (AdcGyroXZ * Vref / 1023 - VzeroRate) / Sensitivitas Persamaan3 RateAyz = (AdcGyroYZ * Vref / 1023 - VzeroRate) / Sensitivitas
AdcGyroXZ, AdcGyroYZ - diperoleh dari modul adc kami dan mereka mewakili saluran yang mengukur rotasi proyeksi vektor R di XZ masing-masing di bidang YZ, yang setara dengan mengatakan rotasi dilakukan di sekitar sumbu Y dan X masing-masing.
Vref - adalah tegangan referensi ADC yang akan kita gunakan 3.3V pada contoh di bawah VzeroRate - adalah tegangan tingkat nol, dengan kata lain tegangan yang dikeluarkan giroskop ketika tidak dikenai rotasi apa pun, untuk papan Acc_Gyro adalah misalnya 1.23V (Anda dapat menemukan nilai ini dalam spesifikasi) Sensitivitas - adalah sensitivitas giroskop Anda dinyatakan dalam mV / (deg / s) sering ditulis sebagai mV/deg/s, pada dasarnya memberitahu Anda berapa banyak mV akan output giroskop meningkat, jika Anda meningkatkan kecepatan rotasi satu derajat/s. Sensitivitas papan Acc_Gyro misalnya 2mV/deg/s atau 0,002V/deg/s
Mari kita ambil contoh, misalkan modul ADC kita mengembalikan nilai berikut:
AdcGyroXZ = 571 AdcGyroXZ = 323
Menggunakan rumus di atas, dan menggunakan parameter spesifikasi papan Acc_Gyro, kita akan mendapatkan:
TingkatAxz = (571 * 3.3V / 1023 - 1.23V) / (0,002V/derajat/dtk) =~ 306 derajat/dtk TarifAyz = (323 * 3,3V / 1023 - 1,23V) / (0,002V/derajat/dtk) =~ -94 derajat/dtk
Dengan kata lain perangkat berputar di sekitar sumbu Y (atau kita dapat mengatakan itu berputar di bidang XZ) dengan kecepatan 306 deg/s dan di sekitar sumbu X (atau kita dapat mengatakan itu berputar di bidang YZ) dengan kecepatan - 94 derajat/dtk. Harap dicatat bahwa tanda negatif berarti perangkat berputar ke arah yang berlawanan dari arah positif konvensional. Dengan konvensi satu arah rotasi adalah positif. Lembar spesifikasi giroskop yang baik akan menunjukkan kepada Anda arah mana yang positif, jika tidak, Anda harus menemukannya dengan bereksperimen dengan perangkat dan mencatat arah putaran mana yang menghasilkan peningkatan tegangan pada pin keluaran. Ini paling baik dilakukan dengan menggunakan osiloskop karena segera setelah Anda menghentikan putaran, tegangan akan turun kembali ke tingkat tingkat nol. Jika Anda menggunakan multimeter, Anda harus mempertahankan laju rotasi konstan setidaknya selama beberapa detik dan mencatat voltase selama rotasi ini, lalu membandingkannya dengan voltase laju nol. Jika lebih besar dari tegangan tingkat nol berarti arah putarannya positif.
Langkah 3: Menggabungkan Akselerometer dan Gyro
Menyatukan semuanya - Menggabungkan data akselerometer dan giroskop
Jika Anda membaca artikel ini, Anda mungkin memperoleh atau berencana untuk membeli perangkat IMU, atau mungkin Anda berencana untuk membuatnya dari perangkat akselerometer dan giroskop yang terpisah.
Langkah pertama dalam menggunakan perangkat IMU kombinasi yang menggabungkan akselerometer dan giroskop adalah menyelaraskan sistem koordinatnya. Cara termudah untuk melakukannya adalah dengan memilih sistem koordinat accelerometer sebagai sistem koordinat referensi Anda. Sebagian besar lembar data akselerometer akan menampilkan arah sumbu X, Y, Z relatif terhadap gambar chip atau perangkat fisik. Sebagai contoh berikut adalah arah sumbu X, Y, Z seperti yang ditunjukkan pada spesifikasi untuk papan Acc_Gyro:
Langkah selanjutnya adalah:
Identifikasi output giroskop yang sesuai dengan nilai RateAxz, RateAyz yang dibahas di atas. Tentukan apakah output ini perlu dibalik karena posisi fisik giroskop relatif terhadap akselerometer
Jangan berasumsi bahwa jika giroskop memiliki keluaran bertanda X atau Y, itu akan sesuai dengan sumbu apa pun dalam sistem koordinat akselerometer, bahkan jika keluaran ini adalah bagian dari unit IMU. Cara terbaik adalah dengan mengujinya. Dengan asumsi Anda telah memperbaiki posisi giroskop relatif terhadap akselerometer. Diasumsikan bahwa batas giro dan akselerometer sejajar satu sama lain, yaitu Anda menempatkan giro pada kelipatan sudut 90 derajat relatif terhadap chip akselerometer. Jika Anda memperoleh papan IMU, kemungkinan besar mereka sudah disejajarkan dengan cara ini. Kami tidak akan membahas dalam artikel ini model di mana giroskop ditempatkan pada sudut yang tidak teratur relatif terhadap akselerometer (katakanlah 45 atau 30 derajat), meskipun ini mungkin berguna dalam beberapa aplikasi.
Berikut adalah urutan sampel untuk menentukan keluaran giroskop mana yang sesuai dengan nilai RateAxz yang dibahas di atas.
- mulai dari menempatkan perangkat dalam posisi horizontal. Baik keluaran X dan Y dari akselerometer akan menghasilkan tegangan nol-g (misalnya untuk papan Acc_Gyro ini adalah 1,65V)
- selanjutnya mulai memutar perangkat di sekitar sumbu Y, cara lain untuk mengatakannya adalah Anda memutar perangkat dalam bidang XZ, sehingga keluaran akselerometer X dan Z berubah dan keluaran Y tetap konstan. - saat memutar perangkat pada kecepatan konstan, perhatikan output giroskop mana yang berubah, output giroskop lainnya harus tetap konstan - output giroskop yang berubah selama rotasi di sekitar sumbu Y (rotasi dalam bidang XZ) akan memberikan nilai input untuk AdcGyroXZ, dari mana kami menghitung RateAxz - langkah terakhir adalah memastikan arah rotasi sesuai dengan model kami, dalam beberapa kasus Anda mungkin harus membalikkan nilai RateAxz karena posisi fisik giroskop relatif terhadap akselerometer - lakukan lagi tes di atas, putar perangkat di sekitar sumbu Y, kali ini pantau output X dari akselerometer (AdcRx dalam model kami). Jika AdcRx tumbuh (rotasi 90 derajat pertama dari posisi horizontal), maka AdcGyroXZ juga harus tumbuh. Jika tidak, Anda perlu membalikkan RateAxz, Anda dapat mencapainya dengan memasukkan faktor tanda dalam Persamaan3, sebagai berikut:
RateAxz = InvertAxz * (AdcGyroXZ * Vref / 1023 - VzeroRate) / Sensitivitas, di mana InvertAxz adalah 1 atau -1
tongkat tes yang sama dilakukan untuk RateAyz, dengan memutar perangkat di sekitar sumbu X, dan Anda dapat mengidentifikasi keluaran giroskop mana yang sesuai dengan RateAyz, dan jika perlu dibalik. Setelah Anda memiliki nilai untuk InvertAyz, Anda harus menggunakan rumus berikut untuk menghitung RateAyz:
RateAyz = InvertAyz * (AdcGyroYZ * Vref / 1023 - VzeroRate) / Sensitivitas
Jika Anda melakukan tes ini di papan Acc_Gyro, Anda akan mendapatkan hasil sebagai berikut:
- pin output untuk RateAxz adalah GX4 dan InvertAxz = -1. - pin output untuk RateAyz adalah GY4 dan InvertAyz = -1
Mulai saat ini kami akan mempertimbangkan bahwa Anda telah menyiapkan IMU Anda sedemikian rupa sehingga Anda dapat menghitung nilai yang benar untuk Axr, Ayr, Azr (sebagaimana didefinisikan Bagian 1. Akselerometer) dan RateAxz, RateAyz (sebagaimana didefinisikan di Bagian 2. Giroskop). Selanjutnya kita akan menganalisis hubungan antara nilai-nilai ini yang ternyata berguna dalam memperoleh perkiraan yang lebih akurat dari kemiringan perangkat relatif terhadap bidang tanah.
Anda mungkin bertanya pada diri sendiri pada titik ini, jika model akselerometer sudah memberi kita sudut kemiringan Axr, Ayr, Azr, mengapa kita ingin repot dengan data giroskop? Jawabannya sederhana: data akselerometer tidak selalu dapat dipercaya 100%. Ada beberapa alasan, ingat bahwa akselerometer mengukur gaya inersia, gaya tersebut dapat disebabkan oleh gravitasi (dan idealnya hanya oleh gravitasi), tetapi mungkin juga disebabkan oleh percepatan (gerakan) perangkat. Akibatnya meskipun akselerometer dalam keadaan relatif stabil, akselerometer masih sangat sensitif terhadap getaran dan kebisingan mekanis pada umumnya. Ini adalah alasan utama mengapa sebagian besar sistem IMU menggunakan giroskop untuk memuluskan kesalahan akselerometer. Tapi bagaimana ini dilakukan? Dan apakah giroskop bebas dari kebisingan?
Giroskop tidak bebas dari kebisingan namun karena mengukur rotasi kurang sensitif terhadap gerakan mekanis linier, jenis kebisingan yang diderita accelerometer, namun giroskop memiliki jenis masalah lain seperti misalnya drift (tidak kembali ke nilai tingkat nol saat rotasi berhenti). Namun demikian dengan rata-rata data yang berasal dari akselerometer dan giroskop kita dapat memperoleh perkiraan yang relatif lebih baik dari kemiringan perangkat saat ini daripada yang kita peroleh dengan menggunakan data akselerometer saja.
Pada langkah selanjutnya saya akan memperkenalkan algoritma yang terinspirasi oleh beberapa ide yang digunakan dalam filter Kalman, namun jauh lebih sederhana dan lebih mudah untuk diterapkan pada perangkat yang disematkan. Sebelum itu mari kita lihat dulu apa yang kita ingin algoritma kita hitung. Nah, itu adalah arah vektor gaya gravitasi R = [Rx, Ry, Rz] dari mana kita dapat memperoleh nilai-nilai lain seperti Axr, Ayr, Azr atau cosX, cosY, cosZ yang akan memberi kita gambaran tentang kemiringan perangkat kita relatif terhadap bidang tanah, kita membahas hubungan antara nilai-nilai ini di Bagian 1. Bisa dikatakan - bukankah kita sudah memiliki nilai-nilai ini Rx, Ry, Rz dari Persamaan 2 di Bagian 1? Ya, tapi ingat bahwa nilai-nilai ini diturunkan dari data akselerometer saja, jadi jika Anda akan menggunakannya secara langsung di aplikasi Anda, Anda mungkin mendapatkan lebih banyak noise daripada yang dapat ditoleransi oleh aplikasi Anda. Untuk menghindari kebingungan lebih lanjut, mari kita definisikan ulang pengukuran akselerometer sebagai berikut:
Racc - adalah vektor gaya inersia yang diukur dengan akselerometer, yang terdiri dari komponen berikut (proyeksi pada sumbu X, Y, Z):
RxAcc = (AdcRx * Vref / 1023 - VzeroG) / Sensitivitas RyAcc = (AdcRy * Vref / 1023 - VzeroG) / Sensitivitas RzAcc = (AdcRz * Vref / 1023 - VzeroG) / Sensitivitas
Sejauh ini kami memiliki satu set nilai terukur yang dapat kami peroleh murni dari nilai ADC akselerometer. Kami akan menyebut kumpulan data ini sebagai "vektor" dan kami akan menggunakan notasi berikut.
Racc = [RxAcc, RyAcc, RzAcc]
Karena komponen Racc ini dapat diperoleh dari data akselerometer, kami dapat menganggapnya sebagai masukan untuk algoritma kami.
Harap dicatat bahwa karena Racc mengukur gaya gravitasi Anda akan benar jika Anda berasumsi bahwa panjang vektor yang didefinisikan sebagai berikut sama atau mendekati 1g.
|Rac| = SQRT(RxAcc^2 +RyAcc^2 + RzAcc^2), Namun untuk memastikan masuk akal untuk memperbarui vektor ini sebagai berikut:
Racc(dinormalisasi) = [RxAcc/|Racc|, RyAcc/|Racc|, RzAcc/|Racc|].
Ini akan memastikan panjang vektor Racc Anda yang dinormalisasi selalu 1.
Selanjutnya kami akan memperkenalkan vektor baru dan kami akan menyebutnya
Istirahat = [RxEst, RyEst, RzEst]
Ini akan menjadi output dari algoritme kami, ini adalah nilai yang dikoreksi berdasarkan data giroskop dan berdasarkan data perkiraan sebelumnya.
Inilah yang akan dilakukan algoritme kami: - akselerometer memberi tahu kami: "Anda sekarang berada di posisi Racc" - kami mengucapkan "Terima kasih, tetapi izinkan saya memeriksa", - lalu perbaiki informasi ini dengan data giroskop serta dengan data Istirahat sebelumnya dan kami menampilkan perkiraan vektor Rest yang baru. - kami menganggap Istirahat sebagai "taruhan terbaik" kami untuk posisi perangkat saat ini.
Mari kita lihat bagaimana kita bisa membuatnya bekerja.
Kami akan memulai urutan kami dengan mempercayai akselerometer kami dan menetapkan:
Istirahat(0) = Racc(0)
Omong-omong ingat Istirahat dan Racc adalah vektor, jadi persamaan di atas hanyalah cara sederhana untuk menulis 3 himpunan persamaan, dan hindari pengulangan:
RxEst(0) = RxAcc(0) RyEst(0) = RyAcc(0) RzEst(0) = RzAcc(0)
Selanjutnya kita akan melakukan pengukuran reguler pada interval waktu yang sama dari T detik, dan kita akan mendapatkan pengukuran baru yang akan kita definisikan sebagai Racc(1), Racc(2), Racc(3) dan seterusnya. Kami juga akan mengeluarkan perkiraan baru pada setiap interval waktu Istirahat(1), Istirahat(2), Istirahat(3) dan seterusnya.
Misalkan kita berada di langkah n. Kami memiliki dua set nilai yang diketahui yang ingin kami gunakan:
Istirahat(n-1) - perkiraan kami sebelumnya, dengan Istirahat(0) = Racc(0) Racc(n) - pengukuran akselerometer kami saat ini
Sebelum kita dapat menghitung Rest(n), mari kita perkenalkan nilai terukur baru, yang dapat kita peroleh dari giroskop dan perkiraan sebelumnya.
Kami akan menyebutnya Rgyro, dan itu juga merupakan vektor yang terdiri dari 3 komponen:
Rgyro = [RxGyro, RyGyro, RzGyro]
Kami akan menghitung vektor ini satu komponen pada satu waktu. Kita akan mulai dengan RxGyro.
Mari kita mulai dengan mengamati hubungan berikut dalam model giroskop kita, dari segitiga siku-siku yang dibentuk oleh Rz dan Rxz kita dapat menurunkan bahwa:
tan(Axz) = Rx/Rz => Axz = atan2(Rx, Rz)
Atan2 mungkin merupakan fungsi yang belum pernah Anda gunakan sebelumnya, mirip dengan atan, kecuali ia mengembalikan nilai dalam rentang (-PI, PI) sebagai lawan dari (-PI/2, PI/2) seperti yang dikembalikan oleh atan, dan dibutuhkan 2 argumen, bukan satu. Ini memungkinkan kita untuk mengubah dua nilai Rx, Rz ke sudut dalam kisaran penuh 360 derajat (-PI ke PI). Anda dapat membaca lebih lanjut tentang atan2 di sini.
Jadi mengetahui RxEst(n-1), dan RzEst(n-1) kita dapat menemukan:
Axz(n-1) = atan2(RxEst(n-1), RzEst(n-1)).
Ingatlah bahwa giroskop mengukur laju perubahan sudut Axz. Jadi kita dapat memperkirakan sudut baru Axz(n) sebagai berikut:
Axz(n) = Axz(n-1) + TingkatAxz(n) * T
Ingat bahwa RateAxz dapat diperoleh dari pembacaan ADC giroskop kami. Rumus yang lebih tepat dapat menggunakan laju rotasi rata-rata yang dihitung sebagai berikut:
RateAxzAvg = (RateAxz(n) + RateAxz(n-1)) / 2 Axz(n) = Axz(n-1) + RateAxzAvg * T
Dengan cara yang sama kita dapat menemukan:
Ayz(n) = Ayz(n-1) + TingkatAyz(n) * T
Ok jadi sekarang kita punya Axz(n) dan Ayz(n). Ke mana kita pergi dari sini untuk mengurangi RxGyro/RyGyro? Dari Persamaan. 1 kita dapat menulis panjang vektor Rgyro sebagai berikut:
|Rgyro| = SQRT(RxGyro^2 + RyGyro^2 + RzGyro^2)
Juga karena kami menormalkan vektor Racc kami, kami dapat mengasumsikan bahwa panjangnya adalah 1 dan tidak berubah setelah rotasi, sehingga relatif aman untuk menulis:
|Rgiro| = 1
Mari kita gunakan notasi sementara yang lebih pendek untuk perhitungan di bawah ini:
x =RxGyro, y=RyGyro, z=RzGyro
Menggunakan hubungan di atas kita dapat menulis:
x = x / 1 = x / SQRT(x^2+y^2+z^2)
Membagi pembilang dan penyebut pecahan dengan SQRT(x^2 + z^2)
x = (x / SQRT(x^2 + z^2)) / SQRT((x^2 + y^2 + z^2) / (x^2 + z^2))
Perhatikan bahwa x / SQRT(x^2 + z^2) = sin(Axz), jadi:
x = sin(Axz) / SQRT (1 + y^2 / (x^2 + z^2))
Sekarang kalikan pembilang dan penyebut pecahan di dalam SQRT dengan z^2
x = sin(Axz) / SQRT (1 + y^2 * z ^2 / (z^2 * (x^2 + z^2)))
Perhatikan bahwa z / SQRT(x^2 + z^2) = cos(Axz) dan y / z = tan(Ayz), jadi akhirnya:
x = sin(Axz) / SQRT (1 + cos(Axz)^2 * tan(Ayz)^2)
Kembali ke notasi kami, kami mendapatkan:
RxGyro = sin(Axz(n)) / SQRT (1 + cos(Axz(n))^2 * tan(Ayz(n))^2)
dengan cara yang sama kita menemukan itu
RyGyro = sin(Ayz(n)) / SQRT (1 + cos(Ayz(n))^2 * tan(Axz(n))^2)
Sekarang, akhirnya kita dapat menemukan:
RzGyro = Tanda(RzGyro)*SQRT(1 - RxGyro^2 - RyGyro^2).
Dimana Tanda(RzGyro) = 1 saat RzGyro>=0, dan Tanda(RzGyro) = -1 saat RzGyro<0.
Salah satu cara sederhana untuk memperkirakan ini adalah dengan mengambil:
Tanda(RzGyro) = Tanda(RzEst(n-1))
Dalam praktiknya, berhati-hatilah ketika RzEst(n-1) mendekati 0. Anda dapat melewatkan fase gyro sama sekali dalam kasus ini dan menetapkan: Rgyro = Rest(n-1). Rz digunakan sebagai referensi untuk menghitung sudut Axz dan Ayz dan ketika mendekati 0, nilai dapat meluap dan memicu hasil yang buruk. Anda akan berada dalam domain angka floating point besar di mana implementasi fungsi tan() / atan() mungkin kurang presisi.
Jadi mari kita rekap apa yang kita miliki sejauh ini, kita berada di langkah n dari algoritma kita dan kita telah menghitung nilai-nilai berikut:
Racc - pembacaan arus dari akselerometer Rgyro kami - diperoleh dari Istirahat(n-1) dan pembacaan giroskop saat ini
Nilai mana yang kita gunakan untuk menghitung perkiraan yang diperbarui Rest(n) ? Anda mungkin menebak bahwa kami akan menggunakan keduanya. Kami akan menggunakan rata-rata tertimbang, sehingga:
Istirahat(n) = (Racc * w1 + Rgyro * w2) / (w1 + w2)
Kita dapat menyederhanakan rumus ini dengan membagi pembilang dan penyebut pecahan dengan w1.
Istirahat(n) = (Racc * w1/w1 + Rgyro * w2/w1) / (w1/w1 + w2/w1)
dan setelah mengganti w2/w1 = wGyro kita mendapatkan:
Istirahat(n) = (Racc + Rgyro * wGyro) / (1 + wGyro)
Dalam forum di atas wGyro memberi tahu kita seberapa besar kita mempercayai gyro kita dibandingkan dengan accelerometer kita. Nilai ini dapat dipilih secara eksperimental biasanya nilai antara 5..20 akan memicu hasil yang baik.
Perbedaan utama algoritma ini dari filter Kalman adalah bahwa bobot ini relatif tetap, sedangkan dalam filter Kalman bobot diperbarui secara permanen berdasarkan kebisingan yang diukur dari pembacaan akselerometer. Filter Kalman difokuskan untuk memberi Anda hasil teoretis "terbaik", sedangkan algoritme ini dapat memberi Anda hasil "cukup baik" untuk aplikasi praktis Anda. Anda dapat menerapkan algoritme yang menyesuaikan wGyro tergantung pada beberapa faktor kebisingan yang Anda ukur, tetapi nilai tetap akan berfungsi dengan baik untuk sebagian besar aplikasi.
Kami selangkah lagi untuk mendapatkan nilai perkiraan yang diperbarui:
RxEst(n) = (RxAcc + RxGyro * wGyro) / (1 + wGyro) RyEst(n) = (RyAcc + RyGyro * wGyro) / (1 + wGyro) RzEst(n) = (RzAcc + RzGyro * wGyro) / (1 + wGyro)
Sekarang mari kita normalkan kembali vektor ini:
R = SQRT(RxEst(n) ^2 + RyEst(n)^2 + RzEst(n)^2)
RxEst(n) = RxEst(n)/R RyEst(n) = RyEst(n)/R RzEst(n) = RzEst(n)/R
Dan kami siap untuk mengulangi loop kami lagi.
Panduan ini awalnya muncul di starlino.com, saya telah melakukan beberapa pengeditan ringan dan memposting ulang dengan izin. Terima kasih Starlino!
Direkomendasikan:
Kontrol Robot Mikro:bit Dengan Akselerometer: 4 Langkah
Kontrol Robot Mikro:bit Dengan Akselerometer: Pada artikel ini kita akan menggunakan kit BitCar TinkerGen untuk membuat robot Mikro:bit dan mengontrolnya menggunakan akselerometer pada papan Mikro:bit lainnya.BitCar adalah mikro:bit berbasis do-it- diri Anda robot yang dirancang untuk pendidikan STEM. Cara merakitnya mudah
MPU 6050 Gyro, Komunikasi Akselerometer Dengan Arduino (Atmega328p): 5 Langkah
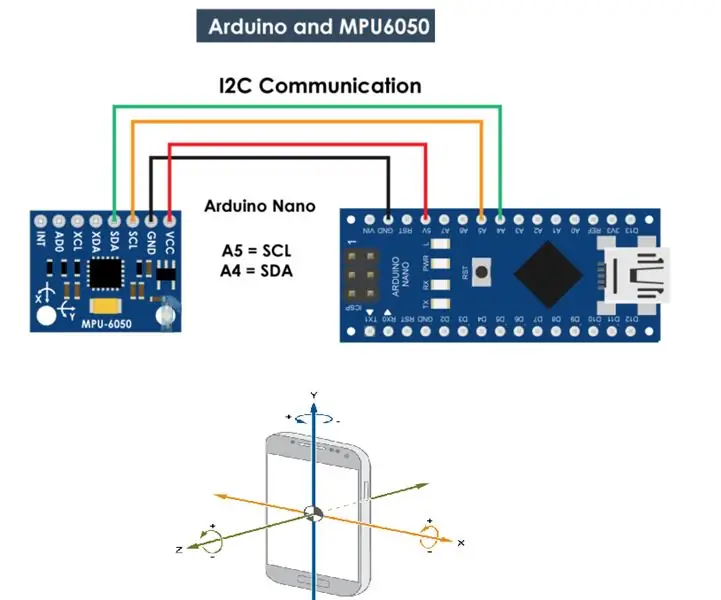
MPU 6050 Gyro, Komunikasi Akselerometer Dengan Arduino (Atmega328p): MPU6050 IMU memiliki akselerometer 3-Sumbu dan giroskop 3-Sumbu yang terintegrasi pada satu chip. Giroskop mengukur kecepatan rotasi atau laju perubahan posisi sudut dari waktu ke waktu, sepanjang sumbu X, Y dan Z. Keluaran dari giroskop adalah
Tutorial Akselerometer Arduino: Mengontrol Jembatan Kapal Menggunakan Motor Servo: 5 Langkah

Tutorial Akselerometer Arduino: Mengontrol Jembatan Kapal Menggunakan Motor Servo: Sensor akselerometer sekarang ada di sebagian besar ponsel cerdas kita untuk memberi mereka berbagai macam penggunaan dan kemampuan yang kita gunakan sehari-hari, tanpa menyadari bahwa yang bertanggung jawab untuk itu adalah akselerometer. Salah satu kemampuan tersebut adalah pengendalian
Tutorial Akselerometer CubeSat: 6 Langkah

Tutorial Akselerometer CubeSat: Cubesat adalah jenis satelit mini untuk penelitian ruang angkasa yang terdiri dari kelipatan 10x10x10 cm kubik unit dan massa tidak lebih dari 1,33 kilogram per unit. Cubesat memungkinkan sejumlah besar satelit dikirim ke luar angkasa dan
Roll and Pitch Axis Gyro untuk GoPro Menggunakan Arduino - Servo dan MPU6050 Gyro: 4 Langkah

Roll and Pitch Axis Gimbal untuk GoPro Menggunakan Arduino - Servo dan MPU6050 Gyro: Instruksi ini dibuat untuk memenuhi persyaratan proyek Makecourse di University of South Florida (www.makecourse.com)Tujuan dari proyek ini adalah untuk membangun sebuah 3-axis Gimbal untuk GoPro dengan menggunakan Arduino nano + 3 motor servo +
