
Daftar Isi:
- Langkah 1: Buat Matriks NxN dari Kuadrat Seragam
- Langkah 2: Mengacak Jaringan
- Langkah 3: Dapatkan Jarak Baru
- Langkah 4: Pilih Titik dan Bandingkan Jarak Dari Titik Itu ke Titik Lainnya
- Langkah 5: Pindah ke Titik Baru
- Langkah 6: Gaya = K*jarak
- Langkah 7: Ubah Gerakan Jaringan Karena Titik yang Dipindahkan
- Langkah 8: Kode Selesai
- Pengarang John Day [email protected].
- Public 2024-01-30 09:57.
- Terakhir diubah 2025-01-23 14:49.

Sel dapat berinteraksi dengan matriks ekstraseluler (ECM) di sekitarnya dan dapat menerapkan serta merespons gaya yang diberikan oleh ECM. Untuk proyek kami, kami mensimulasikan jaringan serat yang saling terkait yang akan bertindak sebagai ECM dan melihat bagaimana jaringan berubah sebagai respons terhadap pergerakan salah satu titik. ECM dimodelkan sebagai sistem pegas yang saling terkait yang awalnya berada dalam kesetimbangan dengan gaya total nol. Ketika gaya diterapkan pada jaringan sebagai respons terhadap pergerakan titik, kami mencoba membuat titik-titik yang terhubung bereaksi terhadap gaya sedemikian rupa sehingga mereka berusaha untuk kembali ke keseimbangan. Gaya dipantau oleh persamaan F=k*x di mana k adalah konstanta pegas dan x adalah perubahan panjang serat. Simulasi ini dapat membantu memberikan pemahaman umum tentang propagasi gaya dalam jaringan berserat yang pada akhirnya dapat digunakan untuk membantu mensimulasikan mekanotransduksi.
Langkah 1: Buat Matriks NxN dari Kuadrat Seragam


Untuk memulai kode, kami memilih N yang akan menentukan dimensi jaringan kami (NxN). Nilai N dapat diubah secara manual untuk mengubah dimensi jaringan sesuai kebutuhan. Dalam contoh ini, N=8 jadi kita memiliki jaringan titik 8x8. Setelah kita membangkitkan matriks, kita menghubungkan semua titik dalam matriks yang memiliki panjang 1 satuan menggunakan rumus jarak, jarak = sqrt((x2-x1)^2+(y2-y1)^2). Dengan melakukan ini, kami mendapatkan jaringan kotak yang semuanya sama-sama berjarak 1 unit. Hal ini dapat dilihat pada gambar 101.
Langkah 2: Mengacak Jaringan


Pada langkah ini, kita ingin mengacak semua lokasi titik kecuali titik terluar yang akan membentuk batas kita. Untuk melakukan ini, pertama-tama kita cari semua koordinat matriks yang sama dengan 0 atau N. Titik-titik inilah yang membentuk batas. Untuk titik non-batas, lokasi diacak dengan menambahkan nilai acak yang berbeda dari -.5 hingga.5 pada posisi x dan y. Gambar acak yang diplot dapat dilihat pada Gambar 1.
Langkah 3: Dapatkan Jarak Baru

Setelah jaringan acak kami dibuat, kami menemukan jarak antara titik-titik yang terhubung menggunakan rumus jarak lagi.
Langkah 4: Pilih Titik dan Bandingkan Jarak Dari Titik Itu ke Titik Lainnya



Pada langkah ini, kita dapat memilih suatu titik tujuan dengan menggunakan kursor, seperti yang ditunjukkan pada Gambar 2. Anda tidak perlu memindahkan kursor tepat ke titik tersebut karena kode akan menyesuaikannya dengan titik koneksi terdekat. Untuk melakukan ini, pertama-tama kita menghitung jarak antara semua titik yang terhubung dan titik yang baru saja kita pilih. Setelah semua jarak dihitung, kami memilih titik dengan jarak terkecil dari titik yang dipilih untuk menjadi titik terpilih yang sebenarnya.
Langkah 5: Pindah ke Titik Baru



Pada langkah ini, dengan menggunakan titik yang dipilih pada langkah sebelumnya, kami memindahkan titik tersebut ke lokasi baru. Gerakan ini dilakukan dengan memilih posisi baru dengan kursor yang akan menggantikan posisi sebelumnya. Gerakan ini akan digunakan untuk mensimulasikan gaya yang diberikan karena perubahan panjang pegas. Dalam gambar semua biru, lokasi baru sedang dipilih. Pada gambar berikut, pergerakan dapat divisualisasikan dengan sambungan jingga yang merupakan lokasi baru dibandingkan dengan sambungan biru yang merupakan lokasi lama.
Langkah 6: Gaya = K*jarak

Pada langkah ini kita menerapkan persamaan gaya=k*jarak, di mana k adalah konstanta 10 untuk serat kolagen. Karena jaringan serat dimulai pada keadaan setimbangnya, gaya totalnya adalah 0. Kami membuat vektor nol dengan panjang matriks yang kami hasilkan sebelumnya untuk mewakili keseimbangan ini.
Langkah 7: Ubah Gerakan Jaringan Karena Titik yang Dipindahkan




Pada langkah ini, kami mensimulasikan pergerakan jaringan sebagai respons terhadap pergerakan titik untuk kembali ke keadaan setimbangnya. Kita mulai dengan mencari jarak baru antara dua titik. Dengan ini kita dapat menemukan perubahan panjang serat dengan melihat perbedaan antara jarak lama dan baru. Kita juga dapat melihat titik mana yang telah berpindah dan juga titik yang terhubung dengannya dengan membandingkan lokasi titik baru dan lama. Ini memungkinkan kita untuk melihat titik mana yang harus bergerak sebagai respons terhadap gaya yang diberikan. Arah gerakan dapat dipecah menjadi komponen x dan y, memberikan vektor arah 2D. Dengan menggunakan nilai k, perubahan jarak, dan vektor arah, kita dapat menghitung vektor gaya yang dapat digunakan untuk memindahkan titik-titik kita menuju kesetimbangan. Kami menjalankan bagian kode ini 100 kali, setiap kali bergerak dengan peningkatan Force*.1. Menjalankan kode 100 kali memungkinkan kita untuk akhirnya mencapai keseimbangan lagi dan dengan menjaga kondisi batas kita melihat perubahan dalam jaringan, bukan hanya seluruh pergeseran. Pergerakan jaringan dapat dilihat pada Gambar 3 dengan warna kuning sebagai posisi yang dipindahkan dan warna biru sebagai posisi sebelumnya.
Langkah 8: Kode Selesai
Terlampir di bagian ini adalah salinan kode kami. Jangan ragu untuk memodifikasinya sesuai kebutuhan Anda dengan memodelkan berbagai jaringan!
Direkomendasikan:
Membuat Grafik Perubahan Suhu Dari Perubahan Iklim dengan Python: 6 Langkah
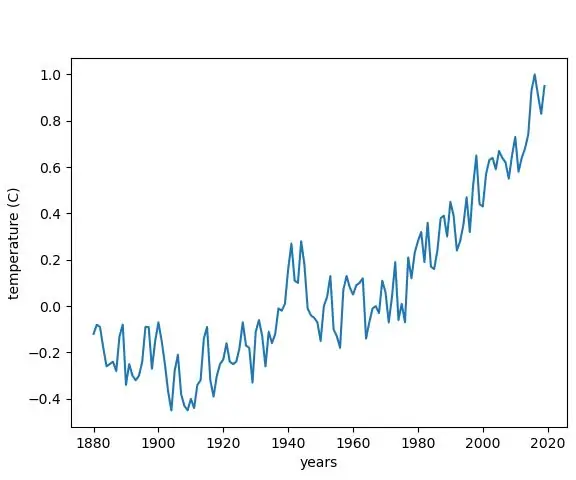
Membuat Grafik Perubahan Suhu Dari Perubahan Iklim dengan Python: Perubahan Iklim adalah masalah besar. Dan banyak orang tidak tahu berapa banyak kenaikannya. Dalam instruksi ini, kami akan membuat grafik perubahan suhu dalam iklim akibat perubahan iklim. Untuk lembar contekan, Anda dapat melihat file python di bawah ini
Input Steker Listrik Super Nintendo Diganti Dengan Gaya Umum.: 5 Langkah

Input Steker Listrik Super Nintendo Diganti Dengan Gaya Umum.: PERINGATAN: JANGAN coba ini jika Anda tidak terbiasa dengan penyolderan & berurusan dengan kekuasaan & sirkuit pada umumnya. SELALU kenakan KACA SAFETY saat melakukan penyolderan atau bekerja dengan alat apa pun. Jangan pernah meninggalkan adaptor daya
Papan Selancar yang Dihasilkan Data: 11 Langkah (dengan Gambar)

Data Generated Surfboards: Ini diambil dari tesis senior saya di Desain Industri dari sekitar setahun yang lalu jadi maaf jika ada beberapa lubang di dalamnya memori saya mungkin sedikit off. Ini adalah proyek eksperimental dan ada begitu banyak hal yang bisa dilakukan secara berbeda, jangan
Membuat HDD Eksternal Dari CD/RW Eksternal Lama: 5 Langkah

Membuat HDD Eksternal Dari CD/RW Eksternal Lama: Konversi langsung dari cd/rw eksternal lama ke hard drive eksternal yang lebih berguna. Persediaan1-cd/rw eksternal (sebaiknya tipe yang lebih berbentuk kotak)1-hard drive (harus sesuai dengan konektor internal casing drive, perlu diformat/disistem)1-sm
Mengonversi Pemutar Mp3 Saya ke Port Usb Langsung dan Baterai yang Dapat Diganti: 3 Langkah

Mengubah Pemutar Mp3 Saya ke Port Usb Langsung dan Baterai yang Dapat Diganti: pada instruksi ini saya akan menunjukkan kepada Anda bagaimana saya mengubah i-pod shuffle saya menjadi memiliki port usb langsung (menggunakan pemutar mp3 ke komputer tanpa menggunakan adaptor) dan untuk ganti baterai bawaan dengan baterai ponsel dan ponsel b
