
Daftar Isi:
- Pengarang John Day [email protected].
- Public 2024-01-30 09:53.
- Terakhir diubah 2025-01-23 14:49.


Berikut adalah aplikasi praktis persamaan matematika kompleks.
Ini sebenarnya adalah teknik yang sangat berguna yang dapat Anda gunakan untuk mengkarakterisasi komponen, atau bahkan antena, pada frekuensi yang telah ditentukan.
Jika Anda telah bermain-main dengan elektronik, Anda mungkin akrab dengan Resistor dan hukum Ohm. R = V / I Sekarang Anda mungkin terkejut mengetahui bahwa hanya ini yang Anda perlukan untuk menyelesaikan impedansi kompleks juga! Semua impedansi pada dasarnya kompleks, yaitu, mereka memiliki bagian Nyata dan Imajiner. Dalam kasus Resistor, imajiner (atau reaktansi) adalah 0, dengan demikian tidak ada perbedaan fasa antara V dan I, jadi kita dapat mengabaikannya.
Ringkasan singkat tentang bilangan kompleks. Kompleks secara sederhana berarti bahwa bilangan terdiri dari dua bagian, nyata dan imajiner. Ada dua cara untuk merepresentasikan bilangan kompleks, misalnya pada gambar di atas, suatu titik dapat ditentukan oleh nilai Real dan Imajiner, seperti di mana garis kuning dan garis biru bertemu. Misalnya jika garis biru berada di 4 pada sumbu X, dan 3 pada sumbu Y, angka ini akan menjadi 4 + 3i, i menunjukkan bahwa ini adalah bagian imajiner dari angka ini. Cara lain untuk menentukan titik yang sama adalah dengan panjang (atau amplitudo) garis merah serta sudut yang dibuatnya dengan horizontal. Dalam contoh di atas ini akan menjadi 5 < 36,87.
Atau garis dengan panjang 5 pada sudut 36,87 derajat.
Dalam persamaan di atas semua parameter, R, V dan I dapat dianggap memiliki bagian imajiner, ketika bekerja dengan resistor nilai ini adalah 0.
Ketika bekerja dengan induktor atau kapasitor, atau ketika perbedaan fasa dapat diukur (dalam derajat) antara sinyal, persamaan tetap sama tetapi bagian imajiner dari nomor harus disertakan. Kebanyakan kalkulator ilmiah membuat bekerja dengan matematika kompleks menjadi sangat mudah, dalam tutorial ini saya akan bekerja melalui contoh pada Casio fx-9750GII.
Pertama, rekap pada persamaan pembagi tegangan resistor.
Sesuai gambar-
Tegangan pada Y adalah arus i dikalikan dengan R2
i adalah tegangan X dibagi dengan jumlah R1 dan R2
Ketika R2 tidak diketahui, kita dapat mengukur nilai lainnya, X, Y, R1 dan menyusun kembali persamaan untuk menyelesaikan R2.
Perlengkapan
Kalkulator ilmiah
Pembangkit sinyal
Osiloskop
Langkah 1: Pengaturan

Mari kita asumsikan kita ingin menghitung induktansi Device Under Test (DUT) pada 1MHz.
Generator sinyal dikonfigurasi untuk output sinusoidal 5V pada 1MHZ.
Kami menggunakan resistor 2k ohm, dan saluran osiloskop adalah CH1 dan CH2
Langkah 2: Osiloskop

Kami mendapatkan bentuk gelombang seperti yang ditunjukkan pada gambar. Pergeseran fase dapat dilihat dan diukur pada osiloskop untuk memimpin dengan 130ns. Amplitudonya adalah 3.4V. Catatan, sinyal pada CH1 harus 2.5V karena diambil pada output pembagi tegangan, di sini ditampilkan sebagai 5V untuk kejelasan, karena ini adalah nilai yang juga harus kita gunakan dalam perhitungan kita. yaitu 5V adalah tegangan input ke pembagi dengan komponen yang tidak diketahui.
Langkah 3: Hitung Fase

Pada 1MHz periode sinyal input adalah 1us.
130ns memberikan rasio 0,13. Atau 13%. 13% dari 360 adalah 46,6
Sinyal 5V diberi sudut 0.. karena ini adalah sinyal input kami dan pergeseran fasa relatif terhadapnya.
sinyal 3.4V diberi sudut +46.6 (tanda + berarti memimpin, untuk kapasitor sudutnya akan negatif).
Langkah 4: Di Kalkulator


Sekarang kita cukup memasukkan nilai terukur kita ke dalam kalkulator.
R adalah 2k
V adalah 5 (EDIT - V adalah 5, nanti dalam persamaan digunakan X! hasilnya persis sama dengan saya memiliki X sebagai 5 di kalkulator saya)
Y adalah tegangan terukur kami dengan sudut fasa, angka ini dimasukkan sebagai bilangan kompleks, cukup dengan menentukan sudut seperti yang ditunjukkan pada layar kalkulator
Langkah 5: Selesaikan Persamaan

sekarang persamaan
(Y * R) / (X - Y)
diketik ke dalam kalkulator, ini adalah persamaan yang persis sama yang kami gunakan untuk menyelesaikan pembagi tegangan resistor:)
Langkah 6: Nilai Terhitung


Kalkulator memberikan hasilnya
18 + 1872i
18, adalah bagian nyata dari impedansi dan memiliki induktansi +1872 pada 1MHz.
Yang bekerja untuk 298uH sesuai dengan persamaan impedansi induktor.
18 ohm lebih tinggi dari hambatan yang akan diukur dengan multimeter, ini karena multimeter mengukur hambatan di DC. Pada 1MHz ada efek kulit, di mana bagian dalam konduktor dilewati oleh arus dan hanya mengalir di bagian luar tembaga, secara efektif mengurangi luas penampang konduktor, dan meningkatkan resistansi.
Direkomendasikan:
Komponen Kompleks Pematrian: 4 Langkah

Pematrian Komponen Kompleks: Pernahkah Anda ingin mendapatkan chip atau komponen acak dari papan sirkuit acak yang Anda miliki? Tentu itu mudah dilakukan dengan hal-hal seperti kapasitor atau LED, tetapi ketika menyangkut hal-hal yang lebih kompleks, itu menjadi sedikit lebih sulit … Dan ketika segalanya menjadi sulit
Menggunakan Papan Sensor Seni Kompleks untuk Mengontrol Data Murni Melalui WiFi: 4 Langkah (dengan Gambar)

Menggunakan Papan Sensor Seni Kompleks untuk Mengontrol Data Murni Melalui WiFi: Pernahkah Anda ingin bereksperimen dengan kontrol gestur? Membuat sesuatu bergerak dengan lambaian tangan? Kontrol musik dengan memutar pergelangan tangan Anda? Instruksi ini akan menunjukkan caranya! Papan Sensor Seni Kompleks (complexarts.net) adalah mikroc
Menghasilkan Nada dari Berbagai Jenis Menggunakan Persamaan Matematika (MathsMusic) Arduino: 5 Langkah

Menghasilkan Nada dari Berbagai Jenis Menggunakan Persamaan Matematika (MathsMusic) Arduino: Deskripsi Proyek:Perjalanan baru telah dimulai di mana ide dapat dengan mudah diimplementasikan menggunakan komunitas open source (Terima kasih kepada Arduino). Jadi begini caranya · Lihatlah ke sekeliling Anda dan amati sekitar Anda · Temukan Masalah yang perlu
Analisis Impedansi Bio (BIA) Dengan AD5933: 9 Langkah
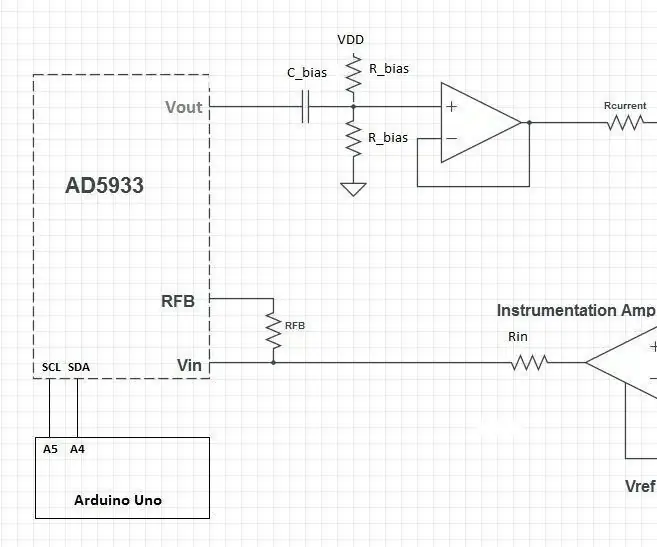
Analisis Impedansi Bio (BIA) Dengan AD5933: Saya tertarik untuk membuat Penganalisis Impedansi Bio untuk pengukuran komposisi tubuh dan pencarian acak saya terus menemukan desain dari kelas Instrumentasi Biomedis 2015 di Universitas Vanderbilt. Saya telah mengerjakan desain dan
Mengukur Impedansi Menggunakan LTspice: 4 Langkah
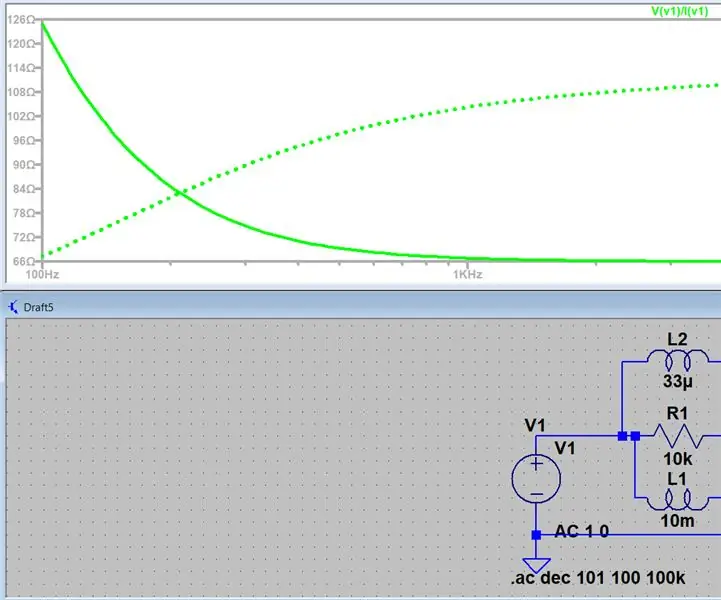
Mengukur Impedansi Menggunakan LTspice: Hai semuanya, ini akan menjadi pengantar sederhana untuk menghasilkan sapuan AC dari suatu rangkaian dan menemukan impedansi pada titik tertentu, ini muncul beberapa kali dalam kursus saya dan sangat sulit bagi saya untuk menemukannya. cara melakukannya secara online jadi
